벨만포드 알고리즘 ( Bellman-Ford Algorithm )

( 본 게시글은 작성자가 메모용으로 사용하는 용도임을 밝힙니다. 정보가 불확실할 수 있으니 참고 부탁드립니다 )

 

벨만포드 알고리즘 ( Bellman-Ford Algorithm )은 가중치가 있는 방향 그래프에서 노드 사이에서의 최단 경로를 찾는 알고리즘이다. 최단 경로를 찾는 알고리즘에는 다익스트라 알고리즘도 있는데, 이 벨만포드 알고리즘의 시간복잡도는 O(VE)로 O((V+E)lgV)인 다익스트라보다 일반적으로 느린 편이다. 그럼에도 이 벨만포드 알고리즘을 쓰는 이유는 해당 알고리즘이 음의 가중치를 허용하기 때문이다.

벨만포드 알고리즘은 음의 가중치를 허용하는 장점이 있지만, 그래프 내에서 존재하는 사이클의 간선에서 음의 가중치가 더 클 경우 무한한 루프를 돌기 때문에, 반드시 탈출 조건을 설정해야한다.

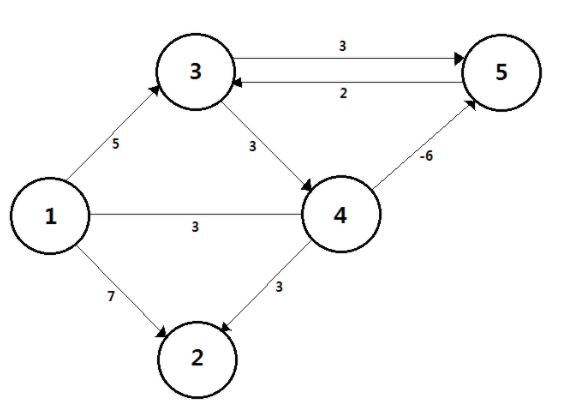
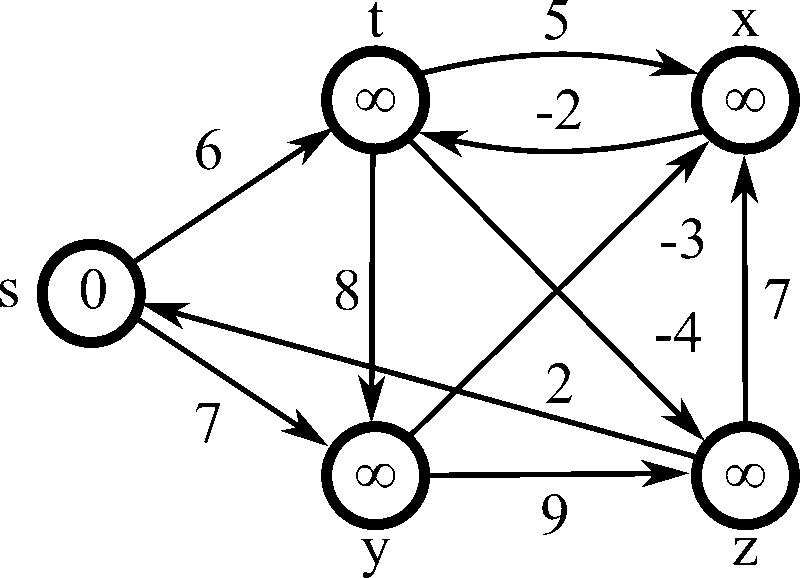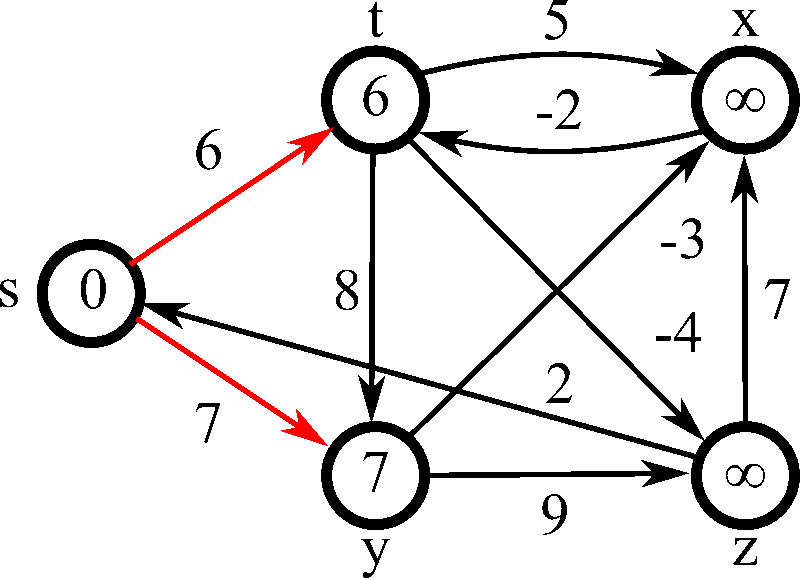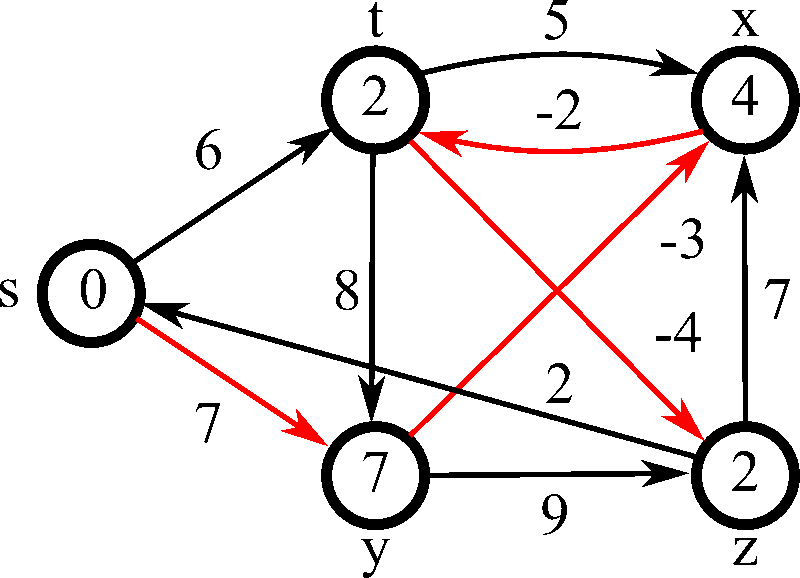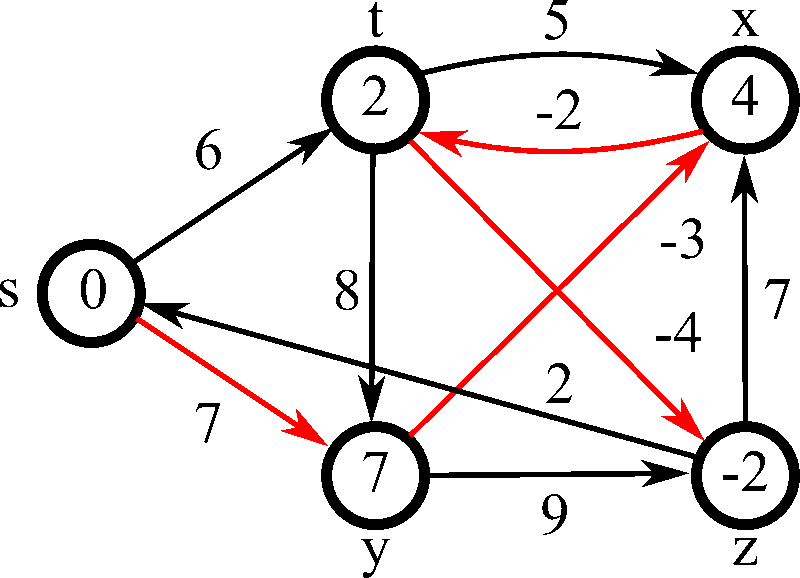
벨만포드의 동작과정은 먼저 출발할 노드를 정해주고, 이외의 나머지 노드들의 거리를 먼저 무한대 ( 혹은 무한대로 볼 수 있는 큰 값 )로 초기화시켜준다. 시작 노드의 거리값은 0으로 둔다. 처음엔 시작 노드의 인접한 노드들부터 탐색하며, 간선의 가중치 값을 노드의 거리값에 갱신한다. 위 같은 경우 시작 노드를 1로 설정한다면 최초 갱신때의 각 노드의 거리값은 2번은 6, 3번은 -1 ( 1 - 4 - 5 - 3 ), 4번은 3, 5번은 -3이 될것이다. 더 이상 값이 줄어들지 않는다면 여기서 멈추겠지만, 음의 가중치로 인해 다시 한번 갱신이 일어난다. 2번 노드의 거리값은 기존 3번 노드 -1에서 4번을 통해서 가면 5로 갱신가능하고, 3번은 4 - 5를 통하면 -2로 갱신, 4번도 5번을 통해 다시오면 2로 갱신, 5번도 -4로 갱신될 것이다. 탐색을 5번 시행한다면 아래처럼 될 것이다.

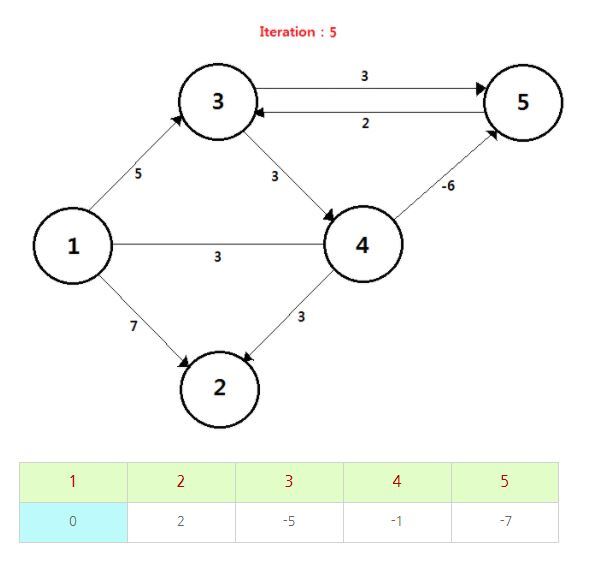
이는 3 - 4 - 5 - 3 사이클의 간선이 음의 가중치가 더 크기때문에, 음수 사이클에 빠졌다고 할 수 있다. 따라서 위에서는 계속 갱신이 무한히 일어날것이다. 이처럼 음수 사이클에 빠지지 않으려면 반드시 탈출 조건을 걸어줘야한다. V - 1개의 노드에 대한 필요 이상의 갱신, 탐색이 일어난다면, 음수 사이클의 존재를 파악할 수 있을 것이다.

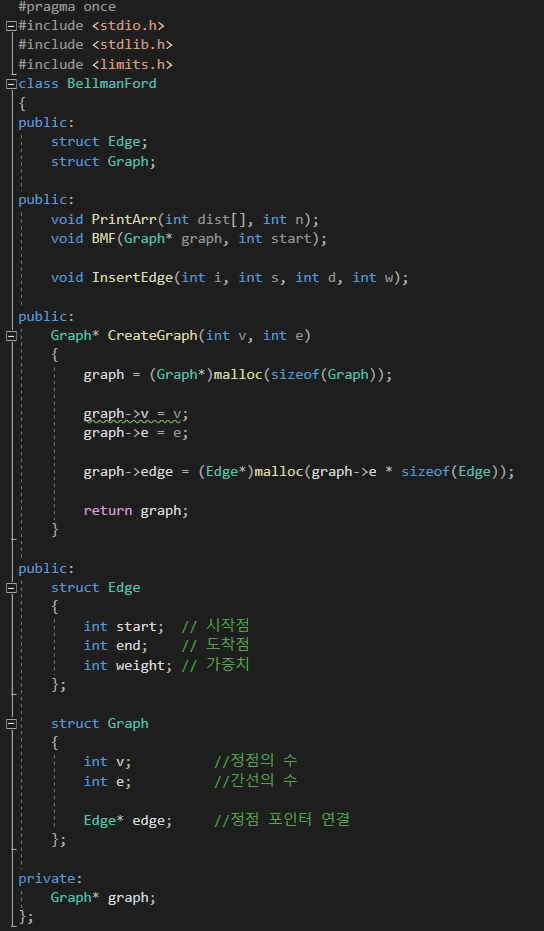
위는 벨만포드 알고리즘의 예제이며, 벨만포드 알고리즘은 클래스로 구현하였고, 간선과 정점은 구현되어있다. main 내에서 직접 정점을 5개, 간선은 9개로 설정했고, 정점간에 가중치를 InsertEdge 함수로 구현하였다. InsertEdge ( 0, 0, 2, 1 )를 예로 들자면, 매개변수 i는 0이기 때문에, 첫번째 간선은 정점 0부터 정점 2까지의 간선을 1의 가중치를 주겠다는 호출이다.

마지막으로 BMF로 그래프를 호출하면 다음과 같이 나올 것이다.

정점 0부터 각 정점까지의 거리가 오른쪽에 표시되어 있다. 위의 그래프를 직접 그림으로 그려보면 다음과 같을 것이다.

위의 그래프에선 음의 사이클은 존재하지 않고, 4번 노드로 가는 방향의 간선은 존재하지 않기 때문에, 4번의 거리값은 무한대로 출력된다.